Lecture 17

最后通牒和讨价还价模型

这个模型一些假设一开始看起来很令人费解。

我们先看模型的一些设定：

• 两个玩家
• 价格总值为1$
• 第一阶段，玩家1会给玩家2一个offer价值s，如果玩家2接受，那么玩家1得到1-s，玩家2会得到s
• 如果玩家2一开始接受，那么游戏结束；如果不接受，那么进入第二阶段，玩家2会提供一个offer $s^{(2)}$，如果玩家1接受了，那么玩家1得到$s^{(2)}$，玩家2得到$1-s^{(2)}$（非常重要的理解方式：这个1-x全都是站在今天的角度的并且一轮就决策好了（玩家2一定同意），如果实际上进行了多轮，提出offer并且被接受那么将会获得全部的奖励）
• 这里有一个折价的设定，如果第一轮玩家2不接受，那么玩家2第二轮最多能得到$\delta$（类似于货币贬值）

两轮

现在假设仅进行两轮游戏，那么玩家1为了在第一轮就能拿到奖励，那么一定就会在第一轮做出丰盛的offer，使得玩家二不会进行第二轮的决策。

那么玩家1给玩家2的奖励一定$\ge \delta$，使得进行一轮就结束了。

三轮

这个时候玩家1被拒绝，玩家2被拒绝，玩家1提出offer。

这个时候的选择路径为：

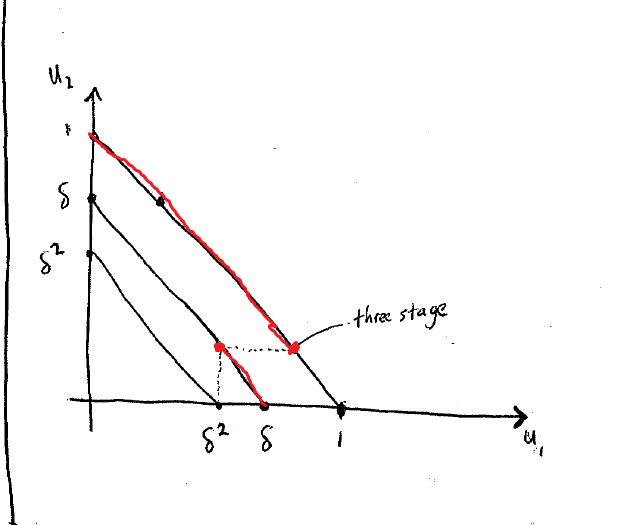
红线表示整个选择的区间，最终为了自己利益的最大，会选择红色的点进行。

收益矩阵

我们计算$s^{\infty} = 1-\delta+\delta^2-\delta^3+\dots +\delta^{\infty} = \frac{1-((-\delta)^{\infty})}{1+\delta} = \frac{1}{1+\delta}$

如果真实的进行n轮，某一轮被同意者获得全部的奖励，但是也会存在者不断的贬值。

再次声明，这样的n轮的推理，实际上是为了就第一轮双方都满意，从而直接得到分配。

假设折价率不是很高，$\delta->1$。

因此双方的收益最终趋近于0.5。与我们直觉是一致的，但是实际上想要得到这样的结果需要诸多的苛刻的条件进行限制。